Abstract
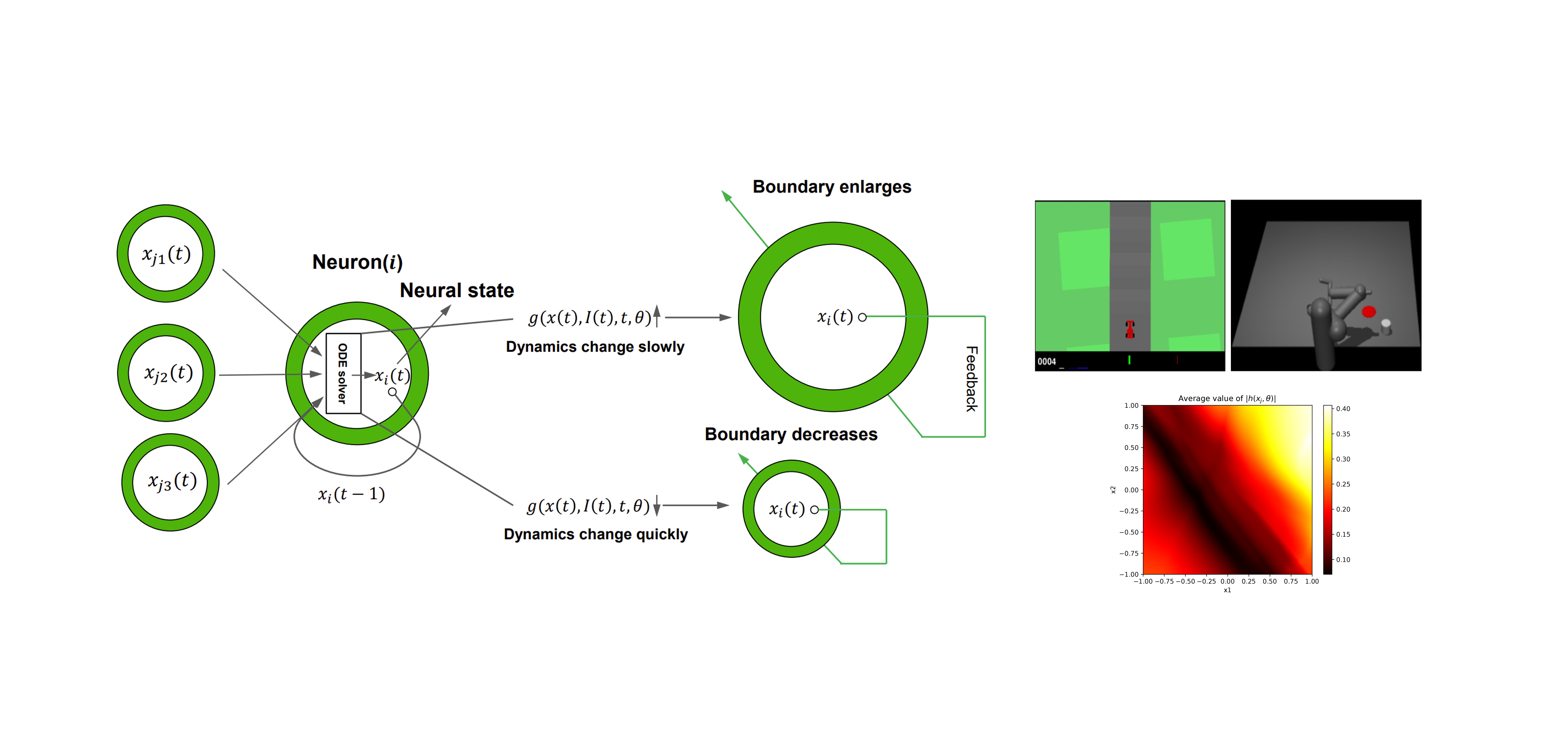
The smoothness of control actions is a significant challenge faced by deep reinforcement learning (RL) techniques in solving optimal control problems. Existing RL-trained policies tend to produce non-smooth actions due to high-frequency input noise and unconstrained Lipschitz constants in neural networks. Current neural ordinary differential equation (ODE) networks have the potential to partially address the smoothing issue through differential equations with low-pass filtering properties, but they fail to directly mitigate control action fluctuations or address smoothing issues deriving from large Lipschitz constant. To address the issue of unsmooth control actions caused by both high-frequency noise and a large Lipschitz constant at same time, we propose the Smooth ODE (SmODE). We first propose a smooth ODE unit that estimates the rate of change in actions near the current state, along with a mechanism that adaptively regulates the boundaries of variations in the neuron hidden states based on these estimates. This effectively minimizes the amplitude of hidden state fluctuations at adjacent time intervals under noisy observational inputs. Therefore, this approach can address the non-smoothing issue associated with large Lipschitz constant. By utilizing smooth ODE unit as neuron, we further advanced the SmODE network serving as RL policy approximators. This network is compatible with most existing RL algorithms, offering improved adaptability compared to prior approaches. Various experiments show that our SmODE network demonstrates superior anti-interference capabilities and smoother action outputs than the multi-layer perception and smooth network architectures like LipsNet.